Какую роль играют вероятности и математика в покере?

Покер - это игра, которая уже долгое время привлекает множество игроков со всего мира. Некоторые рассматривают ее как игру на удачу, где результаты зависят от случайных факторов и распределения карт. Однако настоящие покерные знатоки понимают, что в покере существует значительный элемент стратегии, анализа и принятия решений. Важными инструментами в арсенале покерного игрока являются вероятности и математика.

В данной статье мы рассмотрим роль вероятностей и математики в покере и как эти концепции помогают игрокам принимать информированные решения. Вместо того чтобы полагаться только на удачу, покерные игроки используют вероятности и математические модели для оценки своих шансов на успех и определения оптимальных стратегий.

Будем исследовать основы вероятностей в покере, объяснять различные типы вероятностей, такие как предварительные шансы и текущие шансы, и как они влияют на принятие решений в игре. Кроме того, мы рассмотрим основные математические концепции, используемые в покере, такие как ожидаемая стоимость и математическое ожидание, и покажем, как игроки могут использовать эти концепции для повышения своей выгоды.

Основы вероятностей в покере

Вероятность является ключевым понятием в покере и играет важную роль в принятии решений игроком. Вероятность в покере отражает шансы на получение определенных комбинаций карт или достижение желаемого результата. Понимание вероятности помогает игроку оценить свои шансы на успех и принять информированное решение.

Покерные шансы представляют собой числовые значения, которые отражают вероятность того, что определенное событие произойдет. Шансы измеряются в виде отношения количества благоприятных исходов к общему числу возможных исходов. Например, если у вас есть две карты одной масти в руке, а на столе уже лежит две карты той же масти, то шансы на получение флеш-дро (еще одной карты той же масти) составляют примерно 4 к 1 (4:1).

В покере можно выделить несколько типов вероятностей, которые игроки активно используют:

1. Предварительные шансы (префлоп-шансы): Это вероятность получения определенных комбинаций карт еще до открытия первых трех карт на столе. Например, вероятность получить пару в кармане (две карты одного достоинства) составляет примерно 6%.
2. Текущие шансы: Это вероятность получения нужных карт на следующих улицах (флоп, терн, ривер), учитывая уже открытые карты. Например, если у вас на флопе есть две карты одной масти и вам нужна еще одна карта той же масти, то текущие шансы на флеш-дро составляют примерно 19% к той же масти.
3. Шансы на улучшение: Это вероятность получения лучшей руки на следующих улицах. Например, если у вас есть низкая пара, а на столе лежат карты, которые могут дать вам тройку или выше, то шансы на улучшение руки могут быть велики.

Понимание этих типов вероятностей позволяет игроку принимать обоснованные решения на каждом этапе игры. Например, зная свои текущие шансы на улучшение руки, игрок может принять решение о том, стоит ли продолжать игру, сделать ставку или сбросить карты. Если шансы на улучшение руки высоки, то игрок может решить остаться в игре и продолжить делать ставки. В случае, когда шансы на улучшение руки невысоки, игрок может принять решение сбросить карты и сэкономить свои фишки.

---

Давайте рассмотрим пример вероятностей в покере. Предположим, вы играете в Texas Hold'em и у вас в руке есть две карты: пиковый валет и пиковая дама. На столе уже лежат три общие карты: пиковый туз, трефовый валет и червовая шестерка. Ваша задача - оценить вероятность того, что вы соберете флеш (пять карт одной масти) к моменту окончания игры.

В колоде всего 52 карты, из которых вам уже известны пять: пиковый валет, пиковая дама, пиковый туз, трефовый валет и червовая шестерка. Остается 47 неизвестных карт. Чтобы собрать флеш, вам нужно получить две пиковые карты на двух оставшихся улицах (тёрн и ривер).

На каждой улице будет раздача одной карты из оставшихся 47 карт в колоде. Чтобы оценить вероятность получения пиковой карты на терне, мы можем рассмотреть отношение количества благоприятных исходов к общему количеству возможных исходов. В этом случае у нас есть 9 благоприятных карт (13 пиковых карт в колоде минус 4 уже известных нам), и 38 оставшихся карт в колоде.

Таким образом, вероятность получения пиковой карты на терне составляет 9 к 38 или примерно 23,7%.

После терна наступает ривер, где будет раздана последняя карта. Здесь вероятность получения пиковой карты будет зависеть от оставшегося количества пиковых карт в колоде и общего количества оставшихся карт.

Если мы предположим, что ни одна из оставшихся карт не является пиковой, то в колоде остается 9 пиковых карт и 46 оставшихся карт. Следовательно, вероятность получения пиковой карты на ривере составляет 9 к 46 или примерно 19,6%.

Чтобы оценить вероятность получения флеша к моменту окончания игры, мы можем перемножить вероятности на терне и на ривере:

0,237 * 0,196 ≈ 0,0465 или примерно 4,65%.

Таким образом, в данном примере у вас есть около 4,65% шансов собрать флеш к моменту окончания игры. Это означает, что в среднем вы сможете собрать флеш примерно в 1 из 22 рук с такой начальной комбинацией и условиями на столе.

Зная эту вероятность, вы можете принять решение, основываясь на возможном выигрыше и ставках других игроков. Например, если ставка оппонента высока, а ваша вероятность собрать флеш невысока, то может быть разумным решением сбросить карты и сэкономить свои фишки. В то же время, если ставки невысоки и вы видите выгоду в ожидаемых выигрышах, то ставка может быть оправданной.

Математические концепции в покере

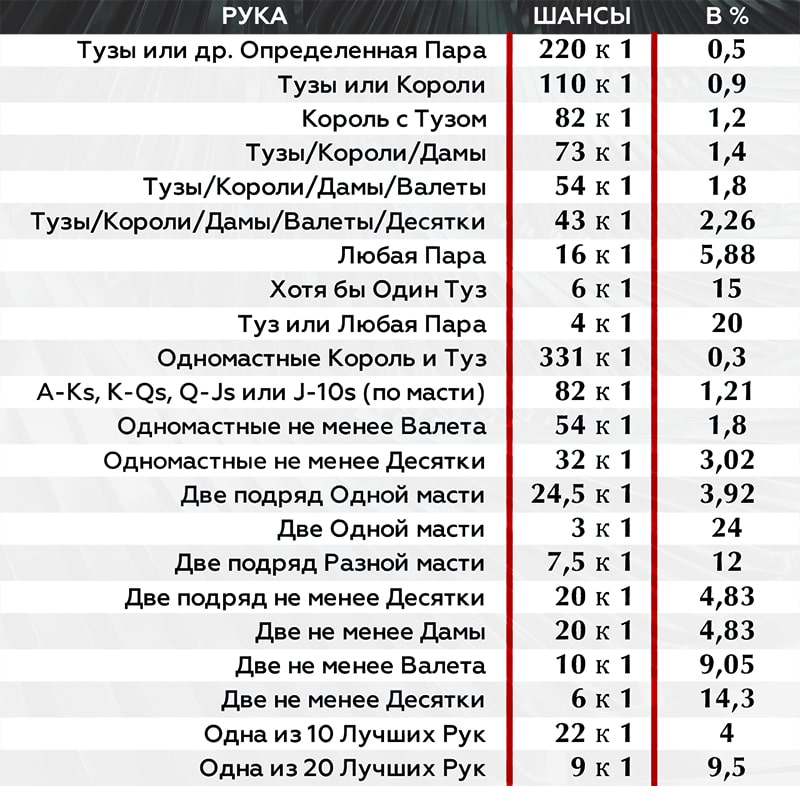
В покере математические концепции играют важную роль и помогают игрокам принимать решения на основе долгосрочной выгоды. Рассмотрим некоторые из этих концепций и их применение в покере.

Ожидаемая стоимость (Expected Value, EV)

Ожидаемая стоимость - это средний выигрыш или проигрыш, который игрок может ожидать в результате своего решения. Она вычисляется путем умножения вероятности каждого исхода на его стоимость и суммирования этих значений. Если ожидаемая стоимость положительна, то решение считается выгодным в долгосрочной перспективе.

Например, предположим, что вы сделали ставку в покере и у вас есть две карты, позволяющие вам собрать флеш на ривере. Вы оценили, что вероятность собрать флеш составляет 20%, а выигрыш в случае его сбора - 100 долларов. Тогда ожидаемая стоимость вашей ставки будет:

(0,2 * 100) + (0,8 * (-50)) = 20 - 40 = -20 долларов.

Это означает, что в среднем ваша ставка приведет к потере 20 долларов. Следовательно, принятие такого решения будет невыгодным в долгосрочной перспективе.

Математическое ожидание

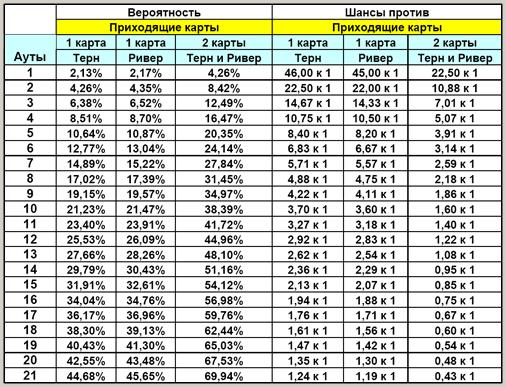
Математическое ожидание - это среднее значение, которое игрок может ожидать в долгосрочной перспективе. Оно вычисляется путем умножения каждого возможного исхода на его вероятность и суммирования этих значений. Математическое ожидание позволяет оценить среднюю результативность определенного решения.

Например, представим, что у вас есть пара в руке, и вы решаете пойти ва-банк. Вероятность выигрыша с такой комбинацией может быть оценена в 30%, а проигрыш - в 70%. При этом выигрыш составляет 200 долларов, а проигрыш - 100 долларов. Тогда математическое ожидание вашей стратегии будет:

(0,3 * 200) + (0,7 * (-100)) = 60 - 70 = -10 долларов.

Среднее значение показывает, что в долгосрочной перспективе вы можете ожидать потери в среднем 10 долларов при использовании данной стратегии. Исходя из этого, может быть разумным пересмотреть свое решение и выбрать более выгодную стратегию.

В итоге, математические концепции играют важную роль в покере, помогая игрокам принимать рациональные решения и оценивать ожидаемую выгоду на долгосрочной основе. Понимание и применение этих концепций позволяют игрокам улучшить свои навыки и повысить свои шансы на успех в покере.

Применение вероятностей и математики при принятии решений в покере

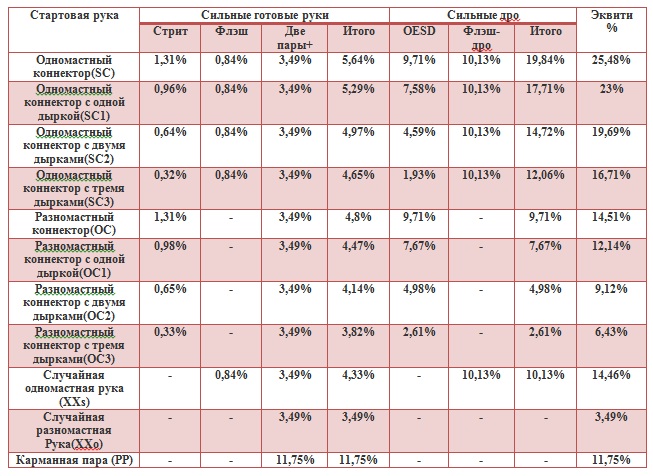
Вероятности и математика играют важную роль при принятии решений в покере. Рассмотрим подробнее и приведем примеры применения этих концепций при принятии решений в игре.

•  * Расчет шансов на победу: Одно из основных применений вероятностей в покере - расчет шансов на победу. Игроки могут использовать вероятности, чтобы оценить свои шансы на собрание выигрышной комбинации или победу в конкретной раздаче. Это помогает им принимать решение о продолжении игры, сделке или сбросе карт.

•  * Принятие решений о ставках: Вероятности также играют важную роль при принятии решений о ставках. Зная вероятность сбора определенной комбинации или улучшения своей руки, игрок может оценить, какие ставки являются выгодными и максимизировать свои ожидаемые выигрыши.

•  * Оптимальные стратегии игры: Математические концепции также используются для разработки оптимальных стратегий игры в покере. Некоторые варианты покера, такие как безлимитный техасский холдем, имеют большое количество возможных решений. Используя математические модели и анализ, игроки могут определить оптимальные диапазоны стартовых рук, размеры ставок и тактику игры в разных ситуациях.

Вероятности и математические концепции играют ключевую роль в покере, помогая игрокам принимать информированные решения и разрабатывать оптимальные стратегии игры. Понимание этих концепций и их применение позволяют игрокам улучшить свои результаты и повысить шансы на успех в покере.

Роль вероятностей и математики в прогнозировании игры соперников

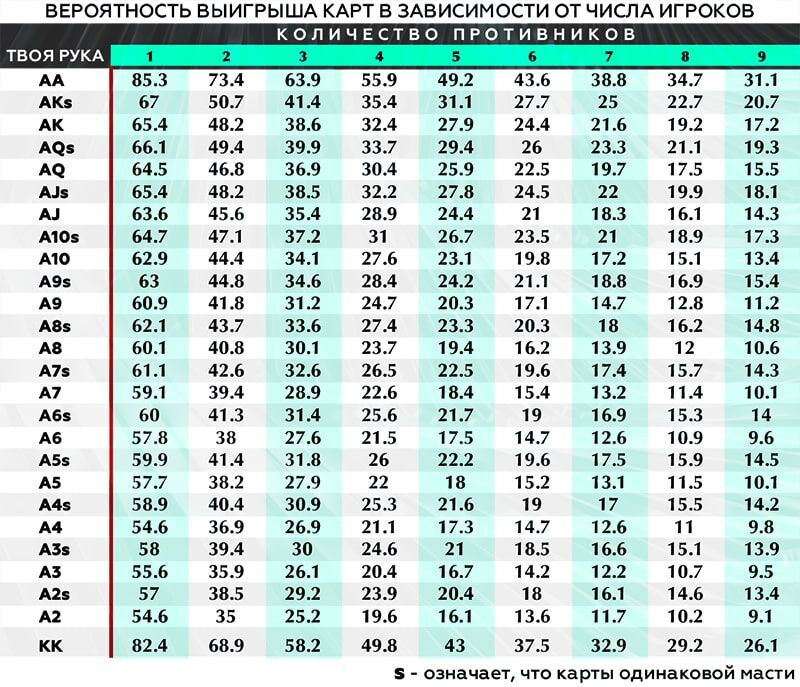
Роль вероятностей и математики в прогнозировании игры соперников в покере неоспорима. Рассмотрим подробнее, какие данные и концепции помогают предсказывать игру соперников и как математика используется для оценки их рейнджей и принятия решений.

•  * Статистические данные: Одним из основных источников информации являются статистические данные, собранные о соперниках во время игры. Это может включать информацию о их ставках, поведении, активности и результатах предыдущих раздач. Анализируя эти данные, игроки могут делать предположения о стиле игры соперников, их предпочтениях и возможных стратегиях.

•  * Рейнджи соперников: Рейндж соперника представляет собой набор возможных комбинаций карт, которые он может иметь на руках в определенной ситуации. Используя вероятностные расчеты и математические модели, игроки могут оценить вероятности различных рук в рейндже соперника и принимать решения на основе этой информации.

•  * Игра на основе математических концепций: Математические концепции, такие как ожидаемая стоимость, математическое ожидание и величина банка, также играют важную роль в оценке игры соперников и принятии решений на основе этой информации. Ожидаемая стоимость (expected value) позволяет игрокам оценивать потенциальные выигрыши или проигрыши при различных решениях и ставках. Путем учета вероятностей и возможных исходов игры, игрок может выбрать наиболее выгодный вариант действий.

Использование вероятностей и математических концепций при прогнозировании игры соперников позволяет игрокам принимать более информированные и обоснованные решения. Это помогает снизить эмоциональное влияние и повышает вероятность долгосрочного успеха в игре. Конечно, в покере существует элемент случайности, но понимание и использование вероятностей и математических концепций помогает игрокам максимизировать свои шансы на успех и улучшить свою игру.

Ограничения и пределы вероятностей и математики в покере

Однако стоит отметить, что вероятности и математика имеют свои ограничения и пределы в покере. Важно понимать, что покер - это игра с неполной информацией, где есть место для воздействия психологических факторов, блефов и принятия решений на основе интуиции и опыта.

•  * Неполная информация: Вероятности и математические модели предполагают наличие полной информации о руке игрока и его соперников. Однако в реальной игре покеристы имеют доступ только к ограниченной информации, такой как собственные карты и открытые карты на столе. Остальная информация о руках соперников остается скрытой. Это делает точное вычисление вероятностей и абсолютное прогнозирование невозможными.
•  * Психология и блефы: Покер - это игра, в которой психологические аспекты игры имеют большое значение. Соперники могут использовать блефы, маскировать свои руки и манипулировать ситуацией, чтобы создать впечатление о своих картах. Эти факторы не поддаются точному математическому анализу. Игроки должны учитывать не только вероятности, но и соперников, их стиль игры, поведение и психологические сигналы.
•  * Вариативность и удача: Покер - игра, где удача играет важную роль. Даже если математические расчеты и вероятности указывают на высокие шансы на успех, всегда есть место для вариации и неожиданных исходов. Ни одна стратегия не гарантирует 100% успеха, и игрокам необходимо быть готовыми к возможным неудачам и учиться адаптироваться к изменяющейся ситуации.

Какую роль играют вероятности и математика в покере? Итоги

Вероятности и математика играют неотъемлемую роль в покере, помогая игрокам принимать информированные решения на основе анализа вероятностей, ожидаемой стоимости и других математических концепций. Основываясь на знании вероятностей, игроки могут оценить свои шансы на победу, принять оптимальные решения о ставках и сделать долгосрочно выгодные ходы.

Основы вероятностей позволяют игрокам оценить вероятность получения определенной комбинации карт, такой как сет или стрит, и принять решение на основе этих данных. Математические концепции, такие как ожидаемая стоимость и математическое ожидание, помогают игрокам определить, какие решения будут наиболее выгодными в долгосрочной перспективе.


Вероятности и математика в покере - это мощный инструмент, который помогает игрокам принимать обоснованные решения, минимизировать риски и максимизировать выгоду. Независимо от уровня игры, понимание и применение вероятностей и математических концепций поможет вам стать более успешным и выигрышным игроком в покере.